时间限制:1000 ms
内存限制:512 MiB
标准输入输出
题目类型:传统
评测方式:文本比较
原题来自:BalticOI 2002
如今的道路收费发展很快。道路的密度越来越大,因此选择最佳路径是很现实的问题。城市的道路是双向的,每条道路有固定的旅行时间以及需要支付的费用。
路径是连续经过的道路组成的。总时间是各条道路旅行时间的和,总费用是各条道路所支付费用的总和。一条路径越快,或者费用越低,该路径就越好。严格地说,如果一条路径比别的路径更快,而且不需要支付更多费用,它就比较好。反过来也如此理解。如果没有一条路径比某路径更好,则该路径被称为最小路径。
这样的最小的路径有可能不止一条,或者根本不存在路径。
问题:读入网络,计算最小路径的总数。费用时间都相同的两条最小路径只算作一条。你只要输出不同种类的最小路径数即可。
第一行有四个整数,城市总数 ,道路总数 ,起点和终点城市 ;
接下来的 行每行描述了一条道路的信息,包括四个整数,两个端点 ,费用 ,以及时间 ;
两个城市之间可能有多条路径连接。
样例输入
4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4
样例输出
样例说明
样例输入如下图:
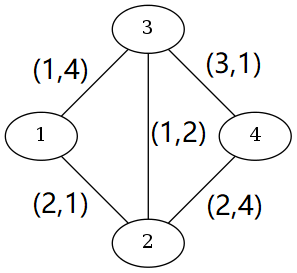
从 到 有 条路径。为 (费用为 ,时间为 ),(费用为 ,时间为 ),(费用为 ,时间为 ),(费用为 ,时间为 )。
和 比 更好。有两种最佳路径:费用为 ,时间为 ( 和 )和 费用为 ,时间为 ()。